Este es un método sencillo, aplicable a canales prismáticos. Divide el canal en tramos cortos y desarrolla los cálculos para cada sección comenzando por una conocida (la sección de control por ejemplo). Si el flujo es subcrítico los cálculos se inician desde aguas abajo y se desarrollan hacia aguas arriba y si es supercrítico se parte de aguas arriba continuándose hacia aguas abajo.
Método de integración directa.
El método del Sr. Bresse es aplicable exclusivamente a canales de sección rectangular donde la relación de ancho (b) a lámina (h) tiende a infinito. Por ello el radio hidráulico (R^) es semejante a la altura hidráulica (Dh) y a su vez es semejante a la lámina (h).
Se debe conocer las siguiente información: caudal (Q); coeficiente de resistencia al flujo (¡zí); pendiente del canal (S0), y las condiciones bien de inicio o de entrega del canal.
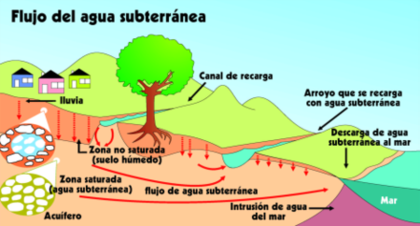
FLUJO SUBTERRANEO
Un modelo de agua subterránea puede ser un modelo a escala o un modelo analógico, por ejemplo un modelo eléctrico basado en la analogía matemática entre el flujo de agua (ley de Darcy) y el flujo de electricidad (ley de Ohm).
Sin embargo, en general, un modelo de agua subterránea se refiere a un modelo de computadora del flujo agua subterránea en sistemas acuíferos usados en la Un modelo de agua subterránea puede ser un modelo a escala o un modelo analógico, por ejemplo un modelo eléctrico basado en la analogía matemática entre el flujo de agua (ley de Darcy) y el flujo de electricidad (ley de Ohm).
Sin embargo, en general, un modelo de agua subterránea se refiere a un modelo de computadora del flujo agua subterránea en sistemas acuíferos usados en la hidrogeología.
El modelo puede incluir los aspectos químicos de la calidad del agua subterránea.
Los modelos de agua subterránea se emplean a menudo para predecir los efectos de cambios hidrológicos, sean naturales o artificiales, en el comportamiento de un acuífero. Se producen cambios artificiales, por ejemplo, por la extracción de agua para uso doméstico, industrial, y/o para regar. Estos modelos también son utilizados para predecir el efecto de la introducción del riego a base de un embalse o un bocatoma. Asimismo, los modelos se utilizan para evaluar los efectos de contaminación química en la superficie del suelo que pueda infiltrar en el acuífero bajo la influencia de la lluvia y lixiviación..
El modelo puede incluir los aspectos químicos de la calidad del agua subterránea.
Los modelos de agua subterránea se emplean a menudo para predecir los efectos de cambios hidrológicos, sean naturales o artificiales, en el comportamiento de un acuífero. Se producen cambios artificiales, por ejemplo, por la extracción de agua para uso doméstico, industrial, y/o para regar. Estos modelos también son utilizados para predecir el efecto de la introducción del riego a base de un embalse o un bocatoma. Asimismo, los modelos se utilizan para evaluar los efectos de contaminación química en la superficie del suelo que pueda infiltrar en el acuífero bajo la influencia de la lluvia y lixiviación.


HIDRÁULICA DE POZOS
Una vez determinadas las posibilidades de producción de agua subterránea en una determinada zona, el siguiente proceso es determinar su adecuada explotación. Para una adecuada producción de los pozos de explotación de los acuíferos fuente, es necesario determinar el uso y así caracterizar de manera económica el beneficio de la explotación del recurso.A continuación, se presentan los diferentes métodos de análisis de pozos en los diferentes tipos de acuíferos existentes. La intención es mostrar el desarrollo matemático de todas las ecuaciones que gobiernan el movimiento del agua subterránea en explotación, ya sea bombeo o recarga de acuíferos. La principal aplicación planteada en este capítulo es la de determinar los radios de influencia de los pozos para así se necesita determinar que interferencia pueden tener entre ellos. Además con los conceptos explicados, se tendrá la capacidad de determinar el abatimiento del nivel freático del acuífero en cualquier punto cuando se esta extrayendo agua.

CONCEPTOS BÁSICOS
Cono de depresión: Al producirse el descenso del nivel estático
del pozo, se establece un gradiente
hidráulico entre cualquier punto de la
formación y el pozo, originándose un
movimiento radial desde todas las
direcciones hacia el pozo en una forma
simétrica y de tal manera que el caudal Q
que se extrae del pozo es igual al caudal
que pasa por cualquier sección del acuífero.
A medida que la velocidad aumenta mayor
será el gradiente hidráulico ya que aumenta
la fricción existente entre el fluido y las
partículas sólidas en contacto; es por eso
que lo que se forma alrededor del pozo se le
conoce como cono de depresión que sobre
un plano vertical presenta una curva
conocida con el nombre de curva de
abatimiento. La forma, alcance y
profundidad de este cono de depresión
dependerá de las condiciones
hidrogeológicas (transmisividad y coeficiente de almacenamiento del acuífero), del caudal y el tiempo de bombeo
o inyección. En el acuífero confinado el cono de depresión es la representación de la variación de los niveles
piezométricos en tanto que en el acuífero libre es además la forma real de la superficie piezométrica.
ƒ
Capacidad Específica: Es la relación que existe entre el caudal que se obtiene de un pozo y el abatimiento producido y se expresa en
unidades de caudal por longitud, [L3/T/L]. Este valor es contante para acuíferos confinados y variables para los
acuíferos libres; es un término que representa el grado de eficiencia de un pozo ya que de dos pozos perforados
en una misma formación acuífera, el de menor capacidad específica tendrá menos eficiencia. El grado de
eficiencia de un pozo lo determinaremos con base en la transmisividad y el coeficiente de almacenamiento de la
formación acuífera, (con la cual podremos calcular un valor de la capacidad específica teórica) el valor de la
capacidad específica real medida en el pozo.
POZOS DE GRAN DIÁMETRO
Los pozos de pequeño diámetro generalmente varían entre 0.05 m y 0.25 m. Como se mostró anteriormente,
esos son representados por una línea en los modelos matemáticos. Esta aproximación es válida para los pozos
en este rango de diámetros, pero inapropiada para pozos con un diámetro mayor. En particular, los radios de
pozos excavados pueden ser de
0.5 m a 2 m o más.
La teoría de Theis asume que el
pozo es una línea en el origen.
Esta suposición no tiene en
cuenta los efectos significativos
de almacenamiento. Los efectos
de este almacenamiento en el
pozo, llegan a ser importantes
cuando la transmisividad y el
coeficiente de almacenamiento
del acuífero son pequeños o
cuando diámetro del pozo de
bombeo es grande.
Papadopulos y Cooper (1967)
desarrollaron soluciones
analíticas en y alrededor de
pozos de gran diámetro en
acuíferos confinados
homogéneos e isotrópicos,
tomando en cuenta los efectos
del almacenamiento dentro del
pozo. Después, Moensch (1985)
presentó modelos matemáticos
que combinaron los acuíferos
semiconfinados de Hantush
(1985) con la teoría antes
mencionada del flujo en pozos de gran diámetro.
No hay comentarios:
Publicar un comentario